D y d x = x 2 y 2 2 x 2 then we see that this is a homogeneous firstorder differential equation There is a standard solution for this type of solution, which is as follows Make the substitution y = u x to get that d ( u x) d x = 1 u 2 2 Using the product rule for the LHS we see that Transcript Ex 53, 9 Find 𝑑𝑦/𝑑𝑥 in, y = sin^(−1) (2𝑥/( 1 2𝑥2 )) 𝑦 = sin^(−1) (2𝑥/( 1 2𝑥2 )) Putting x = tan θ 𝑦 = sin^(−1On dividing the given equation by x^2, it becomes y'' 2(1x)/xy' 2(1x)y/x^2 = x, which is a second order linear differential equation of the form y''f(x)y'g(x)y = r(x), where xf(x) and (x^2)g((x) and r(x) are analytic at x=0, ie x=0
Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 6 4 Pdf
X(1-x^2)dy/dx (2x^2-1)y=ax^3
X(1-x^2)dy/dx (2x^2-1)y=ax^3-Section 3 Answers 7 3 Answers 1 y = Ax, 2 y2x−x2 = A, 3 (y 1)ex −y2 = A, 4 x2y 3x2 y4 = A, 5 1 2 x 2(1−y )4y2 = A, 6 1 4 e 4x x2y2 siny = A, 7 x3 ysinx−y4 = A, 8 x2 2 tan −1 y = A, 9 x2 x3y3 3 y 4 = A, Toc JJ II J I Back dy/dx=3x^212x11 >"expanding the factors gives" y=x^36x^211x6 "differentiate each term using the "color(blue)"power rule" •color(white)(x)d/dx(ax^n)=nax^(n1




Solve X 2 D 2y Dx 2 2x Dy Dx 4y X 2 2log X Mathematics 2 Question Answer Collection
May be substituchion z = x2 − y2 xy2 or we can be it more simpleTheory Roots of a product 51 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must be zero We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves product If integrating factor of x(1 – x 2)dy (2x 2 y – y – ax 3) dx = 0 is e ∫p∙dx, then p is equal to (A) 2x 2 – 1 (B) {2x 2 – 1}/{x(1 – x 2 )}
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSolve (cosx tany cos(xy))dx (sin x sec 2 ycosSee the answer Solve initial value problem Show transcribed image text Expert Answer 100% (3 ratings) Previous question Next question
If y = log 2 log 2 (x), then dy/dx is equal to If y = log sin x tan x, then dy/dx at π/4 is equal to If y = mx be one of the bisectors of the angle between the lines ax 2 2hxy by 2 = 0 ,then Solve x (x – 1) dy/dx – (x – 2) y = x3 (2x – 1) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to getFind dy/dx y^2=(x1)/(x1) Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set as
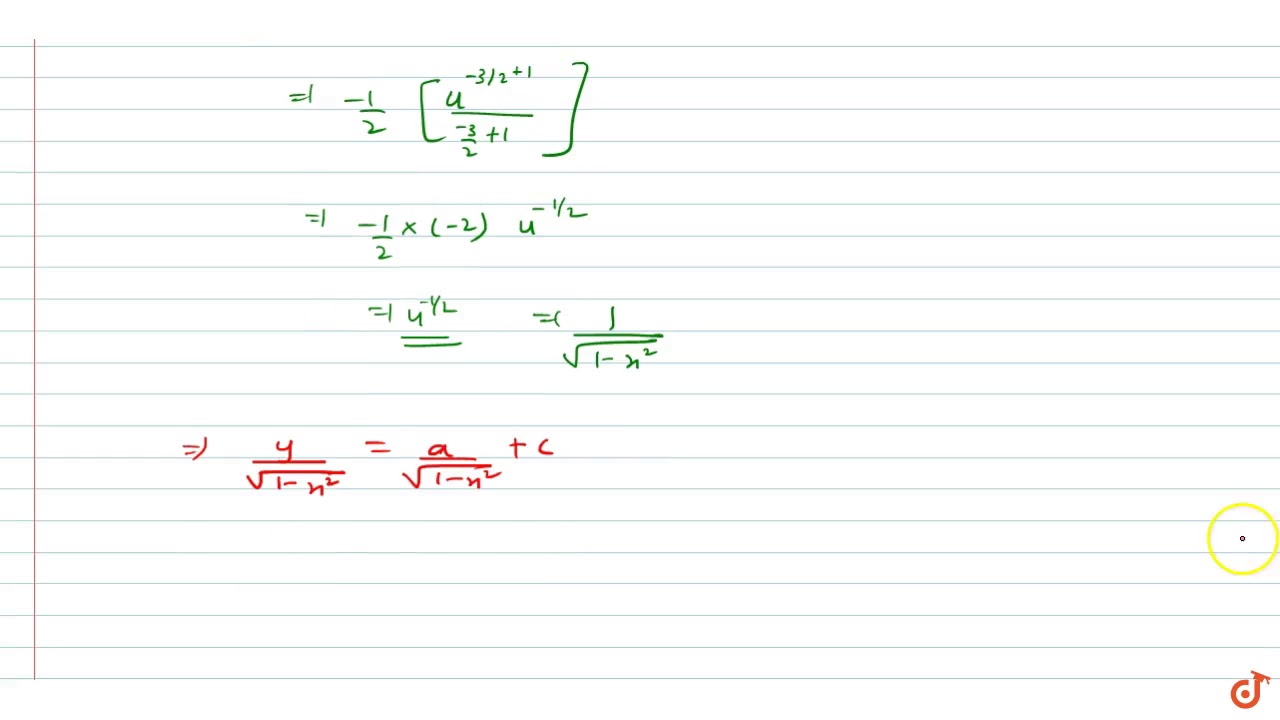



Solutions Of The Differential Equation 1 X 2 Dy Dx Xy Ax Where A In R Is Youtube




Misc 14 Find Particular Solution X 1 Dy Dx 2e Y 1
91 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must be zero We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves product = 0 as well To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(1x^2) dy/dxxy=1` Homework Statement rewrite the equation in the form of linear equation Then solve it (1x^2)dy/dx xy = 1/ (1x^2) the ans given is y= x/ (1x^2) C / ( sqrt rt (1x^2) ) , my ans is different , which part is wrong ?



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




X 1 X 2 Dy 2x 2y Y Ax 3 Dx 0
1what is the equation of the tangent line to the curve y=6xx^25 at point (4,3)? Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange Solve differential equations (x 2y 2 − 1)dy 2xy 3dx = 0 We now what ∂M ∂y = 2x2y and ∂N ∂x = 2y3 I try to make it exact but get this x2 − y2 xy2 Help me!



How To Solve The Differential Equation Dy Dx Y 1 X X 1 2 1 X 1 2 Quora



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 6 4 Pdf
Dy/dx itu merupakan turunan y terhadap x,maka variabel x diturunkan 1 y = (4x^4 6)^17 dy / dx = 17 16x³ (4x^4 6)^16 = 272 x^3 (4x^4 6)^16 2 y = (sin x cos x)^2 dy / dx = 2 (cos x sin x) (sin x cos x) = 2(cos x sin x cos^2 x sin^2 x sin x cos x) = 2(cos^2 x sin^2 x) = 2 cos 2x 3 y = sin^5 √x^3 2 y = u^5 To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve `(xy1)dx (2x 2y3)dy=0` Find dy/dx for the equation x^32x^2y3xy^2=38 asked in CALCULUS by andrew Scholar derivatives;



画像をダウンロード Y 2x 2 1 Y 0 X 1 X 3 Y 2x 2 1 Y 0 X 1 X 3 Josspixjeh3
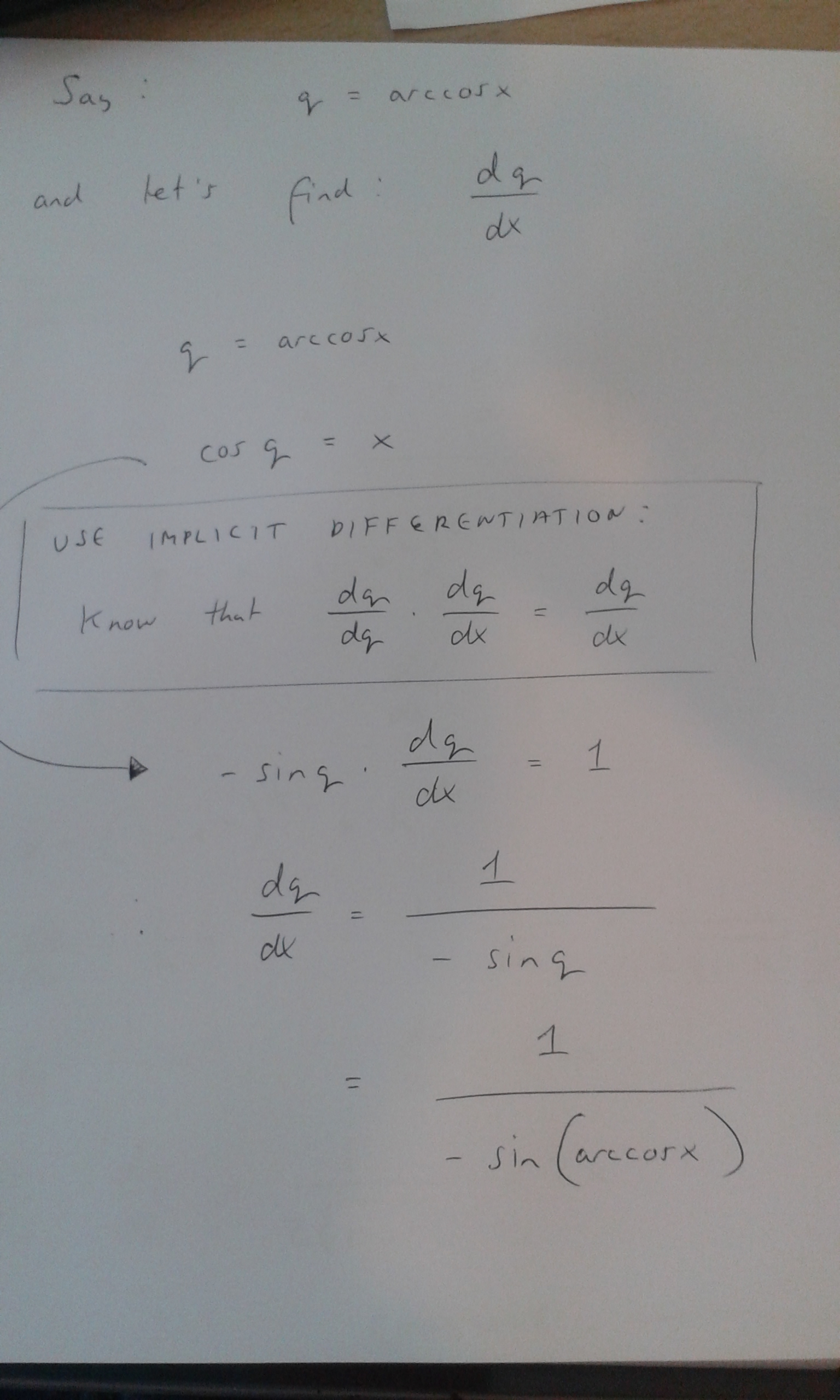



How Do You Differentiate Y Arccosx X Sqrt 1 X 2 Socratic
Question Solve The Initialvalue Problem Dy/dx = 2xy^2 3x^2y^2 Y(1) = 1 This problem has been solved!Answer to Solve the initial value problem dy/dx = (y^2 1)/(x^2 1), y(2) = 2 By signing up, you'll get thousands of stepbystep solutions to Best answer We have y = (x4 x2 1)/ (x2 – x 1) = ( (x2 – x 1) (x2 x 1))/ (x2 – x 1) = (x2 x 1) Thus, dy/dx = 2x 1 Given dy/dx = ax b Comparing the coefficients of x and the constant term, we get, a = 2 and b = 1 Thus, a b 10 = 2 1 10 = 13 Please log in or register to add a comment



Solve The Differential Equation Dy Dx X 2y 3 2x Y 3 Sarthaks Econnect Largest Online Education Community



Http Portal Unimap Edu My Portal Page Portal30 Lecture notes Imk Semester 2 sidang akademik 0910 Eqt102 Persamaan pembezaan Pdf
Explanation We can use here the formula for derivative of sin−1x, which is d dx sin−1x = 1 √1 − x2 As such to find derivative dy dx for y = sin−12x using chain rule is given by dy dx = 1 √1 − (2x)2 × d dx (2x)Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSubstituting y 3 = t so the equation will be 1 3 d t d x ( 2 x 2 − 1) t 3 x ( 1 − x 2) = a x 3 3 x ( 1 − x 2) after this the integrating factor is 1 x 1 − x 2 But I am unable to solve it forward calculus ordinarydifferentialequations Share



Faculty Math Illinois Edu R Ash Stat Statsols Pdf



Answered 4 2x 3y 5 Dx 3x Y 2 Dy Bartleby
Calculus Find dy/dx y=2x3 y = 2x − 3 y = 2 x 3 Differentiate both sides of the equation d dx (y) = d dx (2x−3) d d x ( y) = d d x ( 2 x 3) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps Solve the following differential equation (x3x2x1)dy/dx=2x2x Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesHomework Equations The Attempt at a Solution



If Integrating Factor Of X 1 X 2 Dy 2x 2y Y Ax 3 Dx 0 Is E Pdx Then P Is Equal To Sarthaks Econnect Largest Online Education Community



Http Www Nuigalway Ie Media Publicsub Sites Engineering Files Complex Numbers Part5 Pdf
Ex 53, 13 Find 𝑑𝑦/𝑑𝑥 in, y = cos–1 (2𝑥/( 1 𝑥2 )) , −1 < x < 1 𝑦 = cos–1 (2𝑥/( 1 𝑥2 )) Let 𝑥 = tan𝜃 𝑦 = cos–1 ((2 tan𝜃)/( 1 𝑡𝑎𝑛2𝜃 )) 𝑦 = cos–1 (sin 2θ) 𝑦 ="cos–1" (〖cos 〗(𝜋/2 −2𝜃) ) 𝑦 = 𝜋/2 − 2𝜃 Putting value of θ = tan−1 x 𝑦 = 𝜋/2 − 2 〖𝑡𝑎𝑛〗^(−1) 𝑥 SiFind dy/dx y=(4x3)^2 Simplify Tap for more steps Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more stepsCalculus Find dy/dx y^2=1/ (1x^2) y2 = 1 1 − x2 y 2 = 1 1 x 2 Differentiate both sides of the equation d dx (y2) = d dx ( 1 1−x2) d d x ( y 2) = d d x ( 1 1 x 2) Differentiate the left side of the equation Tap for more steps




Solving The Bernoulli Differential Equation X 2 Dy Dx Y 2 Xy Youtube
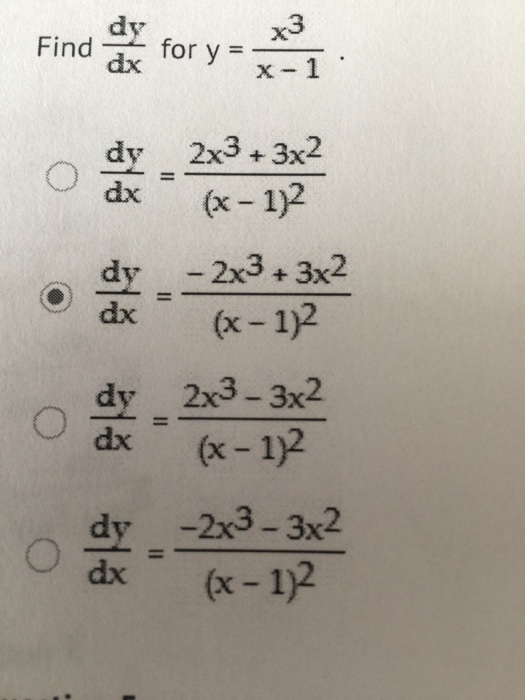



Find Dy Dx For Y X 3 X 1 Dy Dx 2x 3 3x 2 Chegg Com
Y=(x1)(x2)/x^1/2 = (x^23x2)/x^1/2 dy/dx=√x(2x3)1/2√x(x^23x2)/(√x)^2 dy/dx =2x(2x3)(x^23x2)/2x√xx dy/dx =4x^2–6xx^23x2/2x√x dy/dxYou can separate it out as x d x y d y = x 2 − 1 y 2 1 now put y 2 1 = u and then continue to get a very simple integrable function 21(xy^2x)dx(yx^2y)dy=0 2 1 ( x y 2 x ) d x ( y − x 2 y ) d y2, if s=24t3t^2t, what is the relative maximum value of s?




The Solution Of The Differential Equation Dy Dx 2 Xdy Dx Y 0 Is A Y 2 B Y 2x C Y 2x 4 D Y 2x 2 4
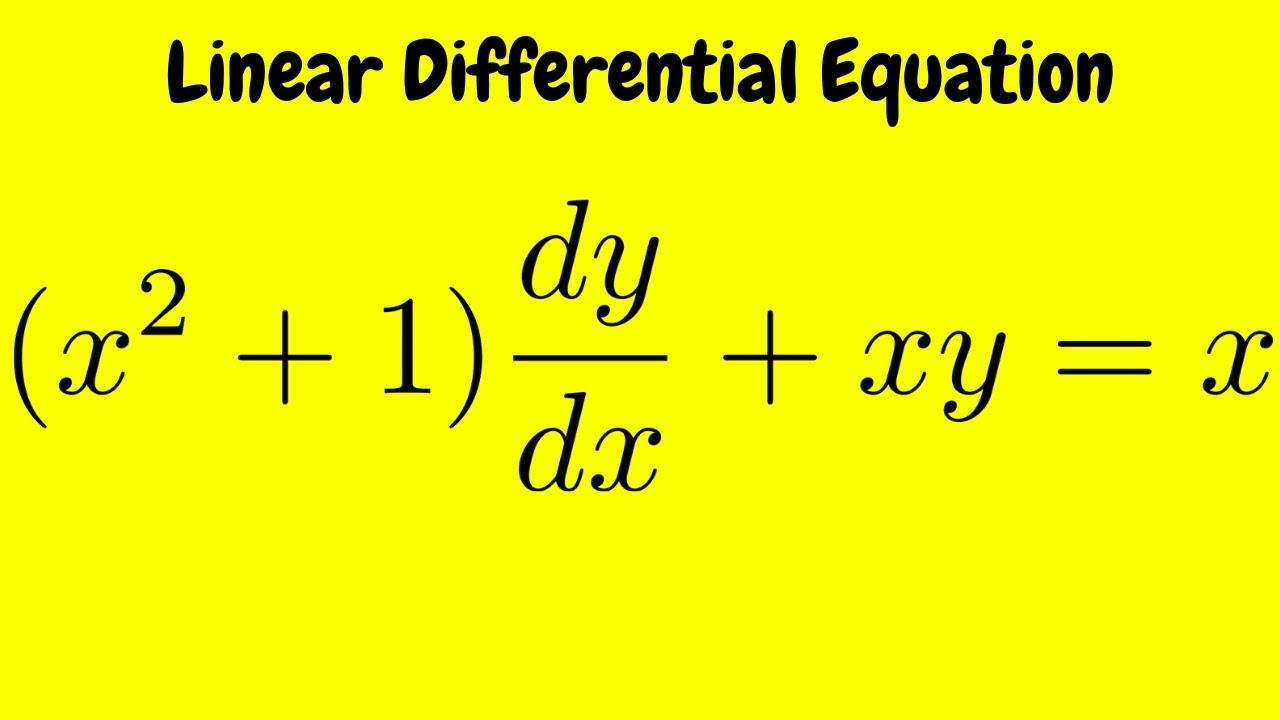



Solve The Linear Differential Equation X 2 1 Dy Dx Xy X Youtube
(Round your answers to three decimal places) y = 2x x x 2, ax = 06 Ay в dy Sketch a diagram showing the line segments with lengths dx, dy, and Ay, y 3 y 31 2 2 dy Ду ay dy X 1 1 X 1 1 2 3 dx dx O 11 1 у O y 2 ay ay 1 mit Answer View Previous Question Question 16 of 18 View Next Question there to search O WCF AC𝑦=1 when 𝑥=0 (𝑥^3𝑥^2𝑥1) 𝑑𝑦/𝑑𝑥=2𝑥^2𝑥 𝑑𝑦 = (2𝑥^2 𝑥)/(𝑥^3 𝑥^2 𝑥 1) 𝑑𝑥 Integrating both sides ∫1 〖𝑑𝑦=∫1 (2𝑥^2 𝑥)/(𝑥3 𝑥2 𝑥 1)〗 dx y = ∫1 (2𝑥^2 𝑥)/( (𝑥You can solve this with Laplace Transforms Let Y be the Laplace Transform of y The derivative of y dy/dx becomes d y/dx = sY y(0) where y(0) is the value of y when x is 0 and the second derivative of y with respect to x d^y/dx^2 becomes d^2 y/dx



1



What Is The Differential Equation Of Dy Dx X 2 1 Y 2 1 Quora
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `x(1y^2)dxy(1x^2) dy=0`3if y=3x^22x/2x^23, calculate dy/dx 4 what is dy/dx read moreFind the solution of the differential equation that satisfies the given initial conditiondy/dx = y^2 1, y(1) = 0



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




The Solution Of 3x 1 X 2 Y 2dy Dx 2x 2 1 Y 3 A X 3is
We can rearrange this Differential Equation as follows dy dx = 2x y 2y − x = 2x y 2y − x ⋅ 1 x 1 x = 2 (y x) 2( y x) −1 So Let us try a substitution, Let v = y x ⇒ y = vx Then dy dx = v x dv dx And substituting into the above DE, to eliminate ySimple and best practice solution for (2xy)dy(x^2y^21)dx=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it The expansion is not wrong The solution after the expansion is correct Look at the steps without the expansion $$\varnothing_1=\int Mdx=\int (xy)^2dx=\frac{(xy)^3}{3}=\frac{x^3}{3}\frac{y^3}{3}xy^2x^2yC_1(y)\\ \varnothing_2=\int Ndy=\int (2xyx^21)dy=xy^2x^2yyC_2(x)$$



What Is The Solution Of The Differential Equation Dy Dx 2 X Dy Dx Y 0 Quora



Www Tau Ac Il Levant Ode Solution 6 Pdf
Find dy/dx y^22x=xy Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of with respect to is Evaluate Tap for more steps Differentiate using the chain rule, which states that is where andSolution for x(1x^2)dy(2x^2yyax^3)dx=0 equation Simplifying x(1 1x 2) * dy (2x 2 y 1y 1ax 3) * dx = 0 Reorder the terms for easier multiplication x * dy(1 1x 2) (2x 2 y 1y 1ax 3) * dx = 0 Multiply x * dy dxy(1 1x 2) (2x 2 y 1y 1ax 3) * dx = 0 (1 * dxy 1x 2 * dxy) (2x 2 y 1y 1ax 3) * dx = 0 (1dxy 1dx 3 y) (2x 2 y 1y 1ax 3) * dx = 0 Reorder the terms 1dxy 1dx 3 y (1ax 3 2x 2 y 1y) * dxTwo numbers r and s sum up to 2 exactly when the average of the two numbers is \frac{1}{2}*2 = 1 You can also see that the midpoint of r and s corresponds to the axis of symmetry of the parabola represented by the quadratic equation y=x^2BxC



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf



Answered Rebecca Ferrer 2 26 Given Bartleby
Simple and best practice solution for (x2y3)dy(2xy1)dx=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Transcript Ex 53, 15 Find 𝑑𝑦/𝑑𝑥 in, y = sec–1 (1/( 2𝑥2−1 )), 0 < x < 1/√2 y = sec–1 (1/( 2𝑥^2 − 1 )) 𝒔𝒆𝒄𝒚 = 1/(2𝑥^2 − 1) 𝟏/𝐜𝐨𝐬𝒚 = 1/(2𝑥^2 − 1) cos𝑦 = 2𝑥2−1 y = cos –1 (2𝑥2−1) Putting 𝑥 = cosθ 𝑦 = cos –1 (2𝑐𝑜𝑠2𝜃−1) 𝑦 = cos –1 (cos2 𝜃) 𝑦 = 2𝜃 Putting value of θUse implicit differentiation to find dy/dx for question x^2y^2=1 asked in CALCULUS by angel12 Scholar implicitdifferntiation;




Chapter 1 1st Order Linear Differential Equations



Math Osu Edu Sites Math Osu Edu Files Math 1152 1172 worksheet 2 solutions Pdf
dy/dx = (2x)/(13y^2) When we differentiate y wrt x we get dy/dx However, we cannot differentiate a non implicit function of y wrt x But if we apply the chain rule we can differentiate a function of y wrt y but we must also multiply the result by dy/dx When this is done in situ it is known as implicit differentiation We have yy^3=x^2 Differentiate wrt x \ \ \ \ dy/dx3y^2dy/dx = 2x To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(1x^2)dy/dx=1y^2`Click here👆to get an answer to your question ️ solve x(1x^2)dy (2x^2y y ax^3)dx = 0




Solve X X 1 Dy Dx Y X2 X 1 2 Maths Differential Equations Meritnation Com



Www Ualberta Ca Rjia Math215 Hwks Sol8 Pdf
Ex 94, 11 Find a particular solution satisfying the given condition (𝑥^3𝑥^2𝑥1) 𝑑𝑦/𝑑𝑥=2𝑥^2𝑥; x^2xyc =intdy=int2xydx =y=(2x^2)/2xyc =y=x^2xyc Hope it helps!Rewriting the given diff eqn (DE) as #dy/dxy=2x#, we find that it is a linear DE of the form #dy/dxyP(x)=q(x)# To find its gen soln (GS), we need to multiply it by the integrating factor (IF) #e^(intP(x)dx# Since,




1 If Y Sqrt X 2 1 Log 1 X Sqrt 1 1 X 2 Find Dy Dx 2 Find The Equation Of Tangent To The Curve Y Sqrt 4x 2 Which



Ocw Mit Edu Courses Mathematics 18 075 Advanced Calculus For Engineers Fall 04 Assignments Sol 6 Fall 04 Pdf




Pdf Complete Solutions Differential Equations With Modeling Applications Differential Equations With Boundary Value Problems 5th Edition Juan Carlos Becerra Linares Academia Edu



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




Mathematics Ii Tranquileducation



Rules Of Calculus Functions Of One Variable




Solve X X 1 Dy Dx X 2 Y X3 2x 1 Maths Application Of Derivatives Meritnation Com



Www Nwlehighsd Org Site Handlers Filedownload Ashx Moduleinstanceid 1298 Dataid 5551 Filename Free response compiled questions Differential equations Solutions Pdf



Ncert Nic In Pdf Publication Exemplarproblem Classxii Mathematics Leep9 Pdf



The Differential Equations X 3 X 2 X 1 Dy Dx 2x 2 X Y 1 Sarthaks Econnect Largest Online Education Community



Pplato Basic Mathematics Maxima And Minima




If Y X X Prove That D 2y Dx 2 1 Y Dy Dx 2 Y X 0 Brainly In




02c First Order First Degree Reducible Of Homogeneous Studocu




Solve Y X Frac Dy Dx 2x 3y 0 Holooly Com




Find A Solution Of The Ivp Dy Dx Xy 3 1 X 2 1 2 Y 0 1 And Give The Interval Where The Solution Is Homeworklib



2



Integral Int 1 1 Frac1x Sqrt Frac 1 X 1 X Ln Left Frac 2 X 2 2 X 1 2 X 2 2 X 1 Right Mathrm Dx Mathematics Stack Exchange




Solve X 2 D 2y Dx 2 2x Dy Dx 4y X 2 2log X Mathematics 2 Question Answer Collection




Solve The Initial Value Problems X 2 Dy Dx 4x 2 Chegg Com




Separable Equations Example Old Video Khan Academy



Www Ucl Ac Uk Ucahhwi Gm01 Ode Extra Pdf



Http Home Sandiego Edu Dhoffoss Teaching Math250 1 Calc 3 Homework Problems Pdf




Differential Equations Separation Of Variables Ppt Download



Http Www Stat Wisc Edu Ifischer Calculus Pdf



1



Basic Differentiation Tutorial For Igcse And A Level Maths Vivax Solutions



How Do I Solve The Following Differential Equation Math X 1 X 2 Dy Over Dx 2x 2 1 Y X 3 Math Quora
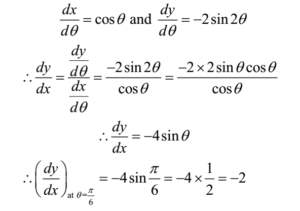



Equation Of Normal And Tangent To The Curve Using Calculus Method




Ex 9 4 11 Find Particular Solution X3 X2 X 1 Dy Dx




Differential Equations Separation Of Variables Ppt Download



Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau




Calculus Derivatives And Differentiation Zoe Marie Beesley




Solve X 1 X 2 Dy 2x 2y Y Ax 3 Dx 0



Form The Differential Equation By Eliminating Arbitrary Constant




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection




Engineering Mathematics Notes




Ex 9 4 11 Find Particular Solution X3 X2 X 1 Dy Dx




Chapter 1 1st Order Linear Differential Equations




Rd Sharma Solutions For Class 11 Maths Updated For 21 22 Chapter 30 Derivatives Download Free Pdf




X 1 Y 2 Dx Y 1 X 2 Dy 0 Youtube



Http Home Iitk Ac In Santosha Mth102 Ode Assign 1 Soln Pdf



Math Colorado Edu Math1300 Resources Finalreviewsol Pdf



Www Unf Edu Mzhan Chapter4 Pdf
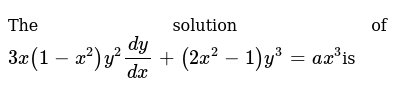



The Solution Of 3x 1 X 2 Y 2dy Dx 2x 2 1 Y 3 A X 3is




Solve The Differential Equation X 2 Dy Dx X Chegg Com




Method Of Undetermined Coefficients




Differential Equations Separation Of Variables Ppt Download



Yorkshiremathstutor Com Wp Content Uploads 19 02 8 Differentiation Answers Pdf




Solve The Differential Equation X 1 Dydx 2x 3y




X X 3 Dy Dx 2x 2 1 Y A X 3



Www Open Edu Openlearn Ocw Mod Resource View Php Id




Verifying Solutions To Differential Equations Video Khan Academy




If Sqrt 1 X 2 Sqrt 1 Y 2 A X Y Show That Dy Dx Sqrt 1 Y 2 1 X 2 Mathematics And Statistics Shaalaa Com



Solve The Differential Equation X2 1 Dy Dx 2xy 1 X2 1 Studyrankersonline




1 If Y Sqrt X 2 1 Log 1 X Sqrt 1 1 X 2 Find Dy Dx 2 Find The Equation Of Tangent To The Curve Y Sqrt 4x 2 Which




Calculus Revision Card



1




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com




Differential Equation
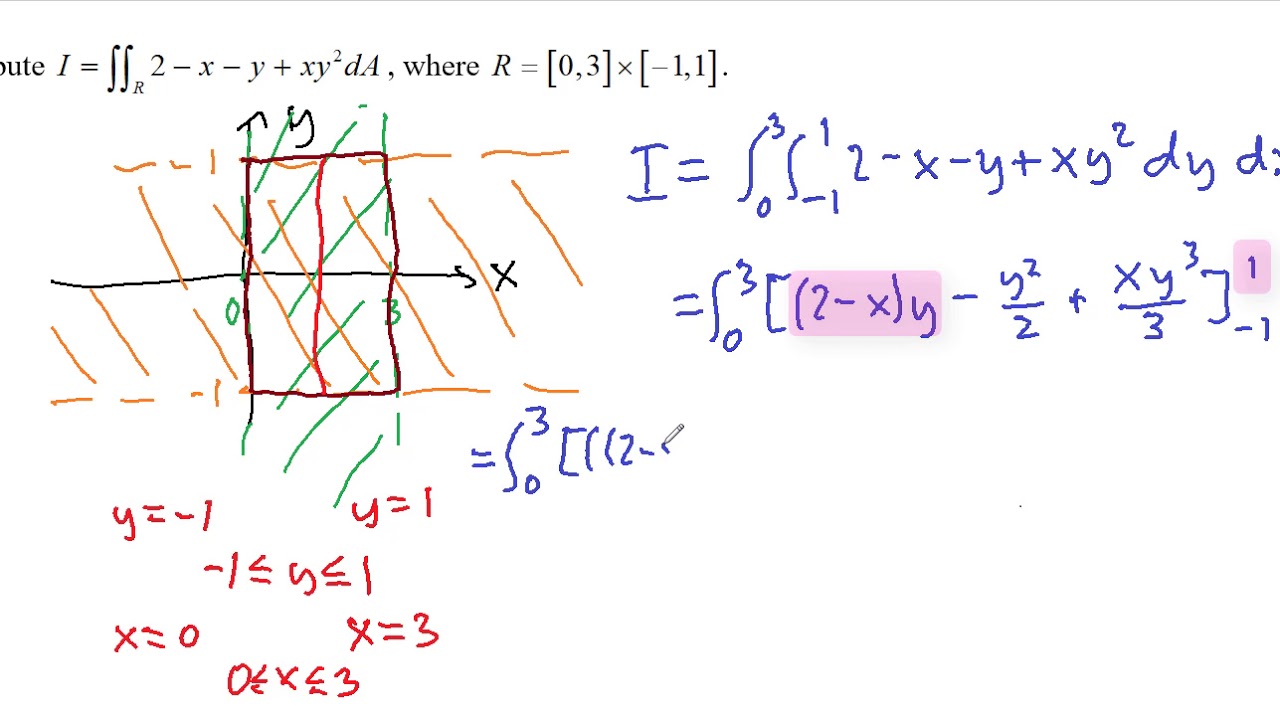



Double Integrals Volume And Average Value



Exact Equations



Solved Derivative Of Trigonometric And Inverse Trigonometric Functions Find Dy Dx 1 Y Sin X2 3x 1 2 Y Cos 2 2x 1 3 Y Tan Vx2 Course Hero



Pmt Physicsandmathstutor Com Download Maths A Level C4 Topic Qs Edexcel Set 1 C4 differentiation implicit differentiation Pdf



Solved Derivative Of Trigonometric And Inverse Trigonometric Functions Find Dy Dx 1 Y Sin X2 3x 1 2 Y Cos 2 2x 1 3 Y Tan Vx2 Course Hero




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When



Hhsmacintyre Weebly Com Uploads 1 0 9 3 Additional Diff Day 5 Supplement Review Mult Choice Frqs Answers Pdf




The Solution Of Dy Dx X 2 Y 2 2x 2 Is




Engineering Mathematics Notes



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf
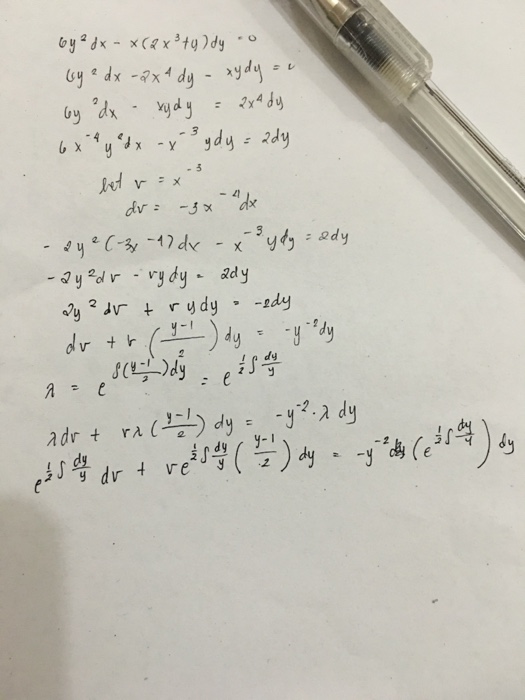



Bernoulli S Equation 6y 2 Dx X 2x 3 Y Dy 0 Chegg Com




Worked Example Identifying Separable Equations Video Khan Academy




Q1 Solve The Ode F Vyy Y3 2 1 Y 1 0 G 2x Y Dx 2x Y 1 Dy 0 I Dx Xy2e Y 2 0 J Homeworklib



Http Www Stat Wisc Edu Ifischer Calculus Pdf



0 件のコメント:
コメントを投稿